| #voters | Their Vote |
|---|---|
| 45 | B>G>N |
| 10 | G>B>N |
| 10 | G>N>B |
| 35 | N>G>B |
| #voters | Their (new) Vote |
|---|---|
| 45 | B>G>N |
| 10 | G>B>N |
| 18 | G>N>B |
| 27 | N>G>B |

These are the slides for WDS lecture delivered at VoComp, Portland OR 17 July 2007. Earlier versions presented at Carnergie-Mellon University, Pittsburgh PA, 17-18 October 2006 and Univ. of Maryland (Baltimore) May 2007.
Abstract.
1. We argue "range voting" is the best single-winner voting method
among all commonly proposed alternatives. Measurements & estimates
indicate
that if adopted instead of the currently most-used system, "plurality voting,"
humanity's lot would improve by an amount comparable to or exceeding the
improvement got from switching from undemocratic forms of government to
democracy. Conservative estimate:
each day's delay in getting range voting
costs (in statistical sense) 5000 lives.
2. We argue (by analysing an explicit political strategy to get it) range voting is, in fact, an obtainable dream.
Speaker is mathematician who co-founded the CRV in 2005.
¶ World decision-making algorithm=bad. Need better one.
¶ Some voting systems including Range Voting (RV)
¶ Arrow impossibility theorem (cannot be a "best" voting system?) – commonly misunderstood and does not even apply to range voting.
¶ Can we actually find a "best" voting system? Objectively compare them? (1) Human historical elections. (2) Darwinian evolution of social species. (3) "Bayesian Regret" methodology.
¶ BR numerical results. How much they really matter.
¶
Can we understand range voting's quality in a more intuitive way?
Honesty.
Expressivity.
Cloning.
Superiority Theorem.
DH3 pathology.
IRV=bad.
¶ "Secondary" effects (e.g. 2-party & 1-party domination, influence of cash, media lapdogism) & Psychology-aided effects
¶ What happens when you try RV on real humans? (Lower spoilage rates)
¶ RV can be done on today's voting machines – no modification & no reprogramming.
¶ How to make it happen – primaries!
¶ Social insects
Major incoming crises:
Important that world make the right decisions. But what is world's decision-making algorithm?
US now sole superpower ⇒ closest simple approximation to the answer = USA's appalling voting system. Features:
|
Systems most commonly mentioned in political science literature illustrated by example:
|
Plurality: A wins (most top-rank votes with 4).
Plurality+Runoff among top two: B wins over A in the runoff, 6-to-5.
Instant Runoff (IRV): C wins
(eliminate E, D, F, and B in that order – doesn't matter which way you break
DF tie – then C beats A in final round 7 to 4).
IRV repeatedly deletes the candidate with fewest
top-rank votes, then the remaining one wins.
Borda: D wins.
(D's Borda score is 16+9+4+5+2=36 versus E with 12+12+6+1+3=34 and
with lower scores for A, B, C, and F.) In the Borda system a candidate gets awarded
0 points if ranked last, 1 if ranked second-last, 2 if... and the candidate
with the greatest score-sum ("Borda count") wins.
Condorcet: E wins. (Since E pairwise-beats each other candidate, e.g. beating
A 6:5, B 6:5, C 7:4, D 6:5, and F 9:2.)
Approval Voting:
If all the red candidates are "approved," then F wins with
7 approvals (versus A=4, B=5, C=3, D=6, E=5).
And with 0-99 Range Voting, it would in fact be possible to make any of the 6 candidates win, depending on how the voters chose the scores compatibly with the orderings above. In Range Voting each voter awards a score from 0 to 99 to each candidate; greatest average score wins. (Fancier rules allow also scoring a candidate with X = intentional blank = "no opinion" – only numerical scores incorporated into averages.)
K.J.Arrow's (1950) theorem states that no voting method can satisfy following short list of conditions:
|
Commonly heard: "Arrow's theorem shows that no 'best' voting system exists."
"Proof":
By Arrow, for every voting system, including the putative "best" system B,
exists an election which makes it look bad. Construct system A which looks good in that situation.
Then A is "superior" to B so B cannot be best. Q.E.D.
That all is wrong. Range voting satisfies all three criteria, accomplishing the "impossible"!
Bogusness. "Property based" thinking misled all of political science for 50 years.
Oversimplified into nutshell: "Bayesian regret" of election method E is "expected avoidable human unhappiness" caused by using E.
More precise answer: Bayesian regret is gotten via this procedure:
Redo steps 1-6 zillion times (i.e. do zillion simulated elections) to find average Bayesian regret of election system E.
Comments: The Bayesian regret of an election system E may differ if we
∃ at least 5 different "knobs" to "turn" on our machine for measuring Bayesian Regret of elctn method E.
Measured Bayesian regrets for about 30 different election methods. 720 different "knob setting" combinations tried. Amazing result: in all 720 scenarios, range voting was best (had lowest Bayesian regret, up to statistically insignificant noise). We repeat: RV best in every single one of those 720 with either honest or strategic voters, regardless of ignorance-level, #candidates (3-5), #voters (5-200), #issues (0-∞) etc.
| Voting system | Regret A | Regret B |
|---|---|---|
| Magically elect optimum winner | 0 | 0 |
| Range (honest voters) | 0.04941 | 0.05368 |
| Borda (honest voters) | 0.13055 | 0.10079 |
| Approval (honest voters) | 0.20575 | 0.16549 |
| Condorcet-LR (honest voters) | 0.22247 | 0.14640 |
| IRV (honest voters) | 0.32314 | 0.23786 |
| Plurality (honest voters) | 0.48628 | 0.37884 |
| Range & Approval (strategic exaggerating voters) | 0.31554 | 0.23101 |
| Borda (strategic exaggerating voters) | 0.70219 | 0.48438 |
| Condorcet-LR (strategic exaggerating voters) | 0.86287 | 0.58958 |
| IRV (strategic exaggerating voters) | 0.91522 | 0.61072 |
| Plurality (strategic voters) | 0.91522 | 0.61072 |
| Elect random winner | 1.50218 | 1.00462 |
Warning: Table makes it appear Borda is second-best after range. But in fact the full study considers hundreds of tables like this, & in many of them, Borda is not second best, in fact in many it's way down in the rankings. The question of which system is second best has no clear answer – some better in some kinds of election situations, others in others.
Less ambitious (but simpler and more reproducible) study: only did the "one-dimensional 3-candidate left-middle-right" political scenario, and very few kinds of voter strategy. But attempted exhaustive set of 623700 configurations, essentially completely covering that space.
Results (some surprises):
Number of voters = 23. Total number of scenarios = 623700. BetterCt[][]:
0 1 2 3 4 5 6 7 8 9 10
RANGE COND PLUR PKING RUNOFF BORDA APPROVAL APRNG WORST BEST RANDOM
0: 0 74096 140855 97481 95160 61600 89724 348 623603 0 623354
1: 23164 0 83007 27911 26539 19214 74446 22604 622834 0 619786
2: 19896 13239 0 22143 11271 32453 87685 19689 616431 0 581325
3: 22189 3246 58393 0 1197 22460 77692 21701 607990 0 597901
4: 22301 4606 60895 14571 0 23820 79052 21805 621036 0 603912
5: 23146 31692 114699 59603 58231 0 55232 22322 622674 0 619190
6: 23288 58942 141949 86853 85481 27250 0 22096 622426 0 602400
7: 1204 74380 141498 97833 95520 61620 89376 0 623606 0 623386
8: 0 0 0 0 0 0 0 0 0 0 0
9: 28918 79832 149525 103473 101767 67354 95336 28062 623700 0 623700
10: 328 3808 42130 25711 19664 4429 21094 296 623700 0 0
|
BR: 2.03 10.9 27.7 17.5 15.6 7.5 18.0 1.94 69.0 0 39.7 |
1. RV=comparable improvement over democracy as invention of democracy. Both transitions non-democracy(modeled by "random winner" or better) → democracy(strategic plurality voting) → Range Voting (halfway between honest & strategic BR numbers) comparable in terms of BR reduction; if anything second looks larger.
2. Democide:
During this [the 20th] century's wars, there were some 38 million battle deaths, but almost four times more people – at least 170 million – were killed by governments for ethnic, racial, tribal, religious, or political reasons. I call this phenomenon democide, and it means that authoritarian and totalitarian governments are more deadly than war.
– R.J.Rummel (prof. Emeritus, U.Hawaii), in his book Death by Government
Rummel on his democide statistics website gives corrections now finding the democide body count during 1900-1999 to be 262,000,000, which is six times the war dead and equiv. to 7200 killed per day.
3. Government waste: Economist Martin Bailey estimates US Govt spending is 50% waste (e.g. same power military could be got with half the money, etc.); detailed tabulation in his book. That 50% is $1.1 Trillion/year, which is equivalent to 4.4 million lives per year, i.e. 12050 lives/day. (At rate of 1 life=$250,000 earned per world-average life).
4. Life expectancy & GNP/capita: Are significantly higher (on average) in democracies. (E.g: [a] Life expectancy in E.Germany jumped 6 years since reunification; [b] Taiwan 77.4 vs China 71 also 6 years; [c] Compare North with South Korea; [d] check Vanhanen's & Barro's large cross-country datasets and fits.) This leads to numbers ≈30,000 lives/day or more.
5. Saving world via better decisions: Suppose USA, by adopting range voting, lowers risk of 2-billion population crash in 50 years, by 5%. That's 5500 lives/day.
Range voting gives you more "bang" for your buck than almost any other philanthropic option. Maybe the most lives saved for this small an effort. And you can be in the steep part of the learning curve by seeding the start of the RV movement, getting huge leverage for your money. (More details)
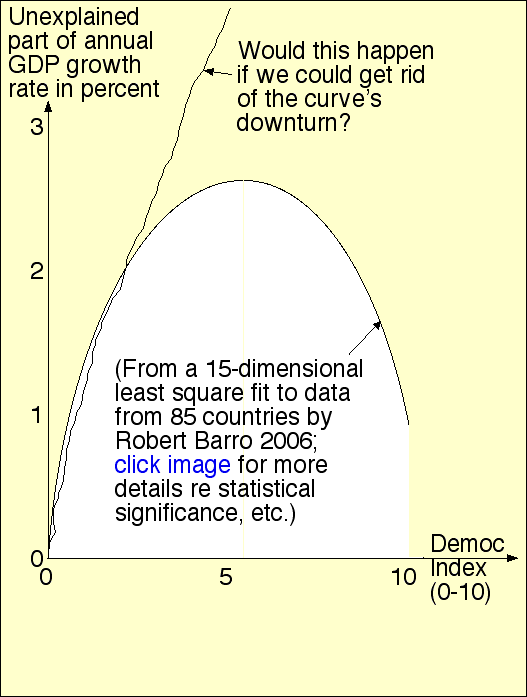
Book R.J.Barro: Determinants of Economic Growth: A Cross-Country Empirical Study predicts growth rate of country's real GDP from facts about country. GDP growth enhanced by:
But democracy increases GDP in peculiar way (pictured): increases in Barro's political rights index from 0 to 5.6 on a scale of 0-10 (yielding a moderate level of freedom and democracy) increased GDP growth rates additively by 2.6% but a further increase in the index from 5.6 to 10 retarded growth by negative 1.6%.
All of Barro's causative factors (listed) cause approximately equal additive effects on predicted real-GDP-growth-rate, namely about 2-5% each. That is, having the optimum level 5.6 of political rights causes about 2.6% higher (additively) annual GDP growth rate than the pessimal level 0; countries about one standard deviation above usual in education levels are predicted to have about 3% higher than usual annual-GDP-growth; etc.
Correlation≠certainty so democracy does not force a good economy. E.g, China doing better than India.
Barro ideologically tries to explain by postulating: more democracy ⇒ more government income redistribution ⇒ hurts growth. But attackable because Barro's fit already had incorporated government expenditures as different predictor; democratization was only being fit to unexplained part of the GDP growth above and beyond that explainable as result of government outlays. Barro partly defends by saying that government transfer payments were not held constant. But, assuming Barro has idea that transfers aim toward equalizing wealth, he is exactly wrong about its economic effect: the Deininger-Squires 1998 World Bank cross-country study found that greater initial inequality is strongly negatively correlated to future economic growth!
In other words, the "trickle down theory" often associated with Ronald Reagan is wrong. According to George R. G. Clarke: More Evidence on Income Distribution and Growth, J. Development Economics 47,2 (Aug. 1995) 403-427, "This conclusion is robust across different inequality measures, and to many different specifications of the growth regression. Furthermore, inequality appears to have a negative effect on both democracies and non-democracies. Interaction terms between inequality and regime type, when included in the base regression, do not affect the sign or significance of [this]." So this seems to settle the matter. (However, to completely clarify matters, it would be good to put transfer payments into Barro's fit also, to see what happens. And two other good predictors to try inserting would be a country's winter temperature and the "centralization fraction" of its government [See A.Lijphart: Democracies 1984 table 10.2 page 178].)
Two other possible explanatory hypotheses: (more supported than Barro's):
There's also psychological reasons, tactical reasons, and "secondary effects"...
Let's look into all these in a little more depth...
Avoids favorite betrayal: In range voting, there is never a strategic reason to give your favorite a non-top score. (Unlike: IRV, Condorcet, Borda, Plurality, where favorite-betrayal often advisable.)
Semi-honesty: In range voting, if you know all other votes (or in a ≤3-candidate election even if you have only partial knowledge of the other votes), then there is always a strategically-optimal "semi-honest" threshold-style vote, where create a "threshold" T and give all candidates better than T score=99, all others score=0. (Unlike: IRV, Condorcet, Borda, Plurality, where it can happen that every honest & semi-honest vote is non-strategic.)
Pleasant surprise theorem: Suppose each voter chooses T=their expectation of the value of the winner. Then: the range-winner will maximize the number of voters who are "pleasantly surprised" (result exceeds expectations). That's an optimality property related to, but not identical to, minimizing Bayesian regret.
Range⇒Condorcet theorem: Suppose each chooses T somewhere between candidates C and A, where C and A are viewed as the two most likely to win. If one of C or A is an honest-voter Condorcet winner, then he will also be the range-winner. (Suggests that in practice, Condorcet cannot have much advantage over range.)
Why? Strategy. Don't want to "waste vote." (⇒ all previous BR studies, with only "honest voters," are of little interest. Also all previous left out RV.)
|
19-voter example illustrating "Favorite Betrayal" & "Condorcet cycle." B wins under vast variety of rank-order election methods (e.g. Borda, Condorcet-LR, IRV).
But if the six N>G>B voters insincerely switch to G>N>B ("betraying their favorite" N) then the "lesser evil" G becomes the winner under all those voting systems – in their view a better election result.
This favorite-betrayal example very important because, once voters understand exaggerating their stances on the apparent-frontrunners can be necessary to prevent "greater evil"s victory, strategic voting is guaranteed, often causing "third parties" to tend to die out (since the strategic voters won't "waste their vote" on honest-favorite third-party candidates like N whom they perceive as having "no chance of winning").
Range Voting: Favorite-betrayal never strategically forced.
|
100-voter example election illustrates: old controversy between Borda and Condorcet (France ≈1780):
|
Condorcet: A should win. (A also wins under IRV voting method.) Borda: no, B should win! Who really should win? Good question.
How would range voting handle this? RV allows voters to say how much they prefer B over A (or whoever). Quantitatively. Really, Borda or Condorcet are both right – but depending on intensity-of-preference information unavailable to their voting methods, but available to range voting. So this example illustrates an advantage of range voting over both previous voting systems.
|
|
|
A 5-voter example. Borda totals: A=9, B=8, C=7, D=6. Reversed Approval counts: A=1, B=2, C=3, D=4! (Generalizes to N candidates.) Both Borda and Approval clueless; range voting (with extra intensity info) can do something sensible.
Several near-identical "clone" candidates run. Plurality voting: they split the vote and all lose. The very popularity of a view can cause its defeat! Borda voting (basically): enough clones ⇒ opposite effect ("teaming"); assured victory!
|
|
Cloning the Bores ⇒ huge advantage! Boring party can just arrange for mucho Bores to enter the race & totally Boring! Of course, Mushites could try to defeat that by intentionally lying in their votes by ranking Bores in opposite of true order, to try to cancel out the Borites and make Mush win. But this strategy causes them to be massively dishonest in their votes and risk not only a Bore-victory, but in fact a victory by the worst of the Bores! (Which would in fact happen if the Borons counterstrategized by also being dishonest in their Bore-orderings!) Crazy!
Mushites: fight by nominating own clones, Mush1, Mush2, Mush3, and Mush4, so they'll win. Bores: countersponsor more clones Bore4, Bore5, Bore6. Etc. War of clone armies. All about gall, little to do with what voters actually want.
Has caused parties to intentionally aid opponents of their point of view ("helping a spoiler")! And it also has (more often) caused parties to intentionally hurt allies of their point of view!
Range Voting: clones & "vote splitting" don't matter, election result not affected. Can't manipulate the election by creating or abolishing clones.
Theorem (WDS 2007): Every reasonable(*) voting method based on rank-order votes is vulnerable either to candidate cloning or to favorite-betrayal. But range voting has neither defect.
(*) "Reasonable" = No "dictator," symmetric under candidate renaming, deterministic aside from tiebreaks which (if any) are random equally likely.
4 candidates and 7 voters. Start looking at situation on left.
|
|
Range Voting: Removing a loser (from all ballots & the election) never changes anything.
Common scenario: Whenever there are 3 rival contenders A,B,C plus one or more "dark horses" D that all agree are worthless no-hopers: In Borda & most Condorcet systems it pays for each for the 3 factions to dishonestly rank D "above" the other two rivals. (Strategic justification: Whichever faction votes honestly, guaranteed to lose the election. Condorcet systems with equal rankings allowed? Ranking D co-equal-last like A>B=C=D is not good enough strategy; only "full force" dishonesty A>D>B>C is strategic.)
|
|
But – Worst possible disaster result: if enough voters do that, D wins.
(DH3 resembles "spoiler pathology" & game of "chicken."
But it's worse. And probably more common.)
Range, IRV, plurality: immune to DH3.
I. IRV leads to 2-party domination (but the closely related top-2-runoff two-round system leads to ≥3 parties). (For voters too dumb to appreciate this, often they'll probably just exaggerate ("Bush is the best! Gore is the worst" out of dumbness anyhow; same effect as being smart.)
|
|
 |
 |
B wins lefthand 100-voter example IRV election. (G, with the fewest top-rank votes, is eliminated in 1st round then B wins 55 to 45 over N.) Realistic scenario from voters and candidates positioned along 1-dimensional line.
At right, suppose 8 voters in bottom faction cleverly (but dishonestly) switch their top-2 preference order. Then N is eliminated in the first round, and then in the second round G wins over B 73-to-27. From those 8 voters' point of view, this was an improvement. Betraying Nader Pays in IRV. Voting Nader causes spoiler effect still in IRV.
|
II. In this 24-voter IRV election, A wins after C is dropped. But now suppose every voter reverses his preference order (now attempting to choose worst rather than best). In that case A still wins after B is eliminated. I.e. IRV contradicts itself; IRV's unambiguously "best" candidate A is here the same as its "worst"!
Also illustrates bizarre kind of strategic voting: Suppose 3 of the B>C>A voters reverse their votes to A>C>B (or alter them to A>B>C; that also works). Then B is eliminated whereupon C wins 13-to-11 over A. The raising of A from bottom-to-top in their vote caused A to lose – and voting maximally dishonestly as though they were suicidally trying to elect the worst candidate, was actually optimal strategy!
Also illustrates "no show paradox": If those three B>C>A voters had simply refused to vote, then C would have won (an improvement in their view). Different way of saying the same thing: these three voters' decision to cast an honest A-last vote caused A to win.
"Primary" effect (reckoned using Bayesian regret): just who wins the election & how much utility that is. "Secondary" effects exert themselves over historical time in sequence of many elections. When these also reckoned, RV looks even better...
2-party domination: In systems where "favorite betrayal" common enough, "2-party domination" happens (third parties die out). 2PD quickly became massive (>99.5%) in the USA (plurality voting) since "idiotic to waste vote by voting Nader." 2PD also experimentally has always happened under IRV, despite moronic propaganda (Australia, Ireland, Fiji). 2PD has not happened under plur+top-2-runoff. ("Duverger's laws.") 2PD might happen under Condorcet systems.
Consequent diminution of voter choice: Bush & Kerry: pro, versus all third-party canddts against: PATRIOT act, WTO, NAFTA, "war on drugs," Iraq war, subsidy-laden "farm bill," (tax cuts leading to) huge budget deficit.
One-party domination: 98% predictability in contemporary USA. (One reason is gerrymandering... by which one party can stay permanently in power even if only 25+ε% support.)
Cash: is extremely important in plurality voting, but perceived to be less so in other systems e.g. plur+top-2-runoff. Why? Need to demonstrate you are one of the top-2 "frontrunners," i.e. create illusion of winnability, otherwise not worth wasting vote on you. That's expensive. (Educating about issues: cheap.)
Media: Pays no attention to third-party views (no motivation; they're not news). Media "lapdogs" unquestioningly accept politicians' BS without much critical examination (because with 2-party and 1-party domination, politicians are in monopoly position to cut off media lifeblood; with multiparties no such info monopoly)
Lack of congressional oversight: For most of about 8 years, Democrats in Congress haven't been able to subpoena anyone.
Rubberstamped agency heads & judge appointments: In votes for court of appeals nominees, Republican Senators during the Bush administration (during majority control) produced 2703 votes for the nominee as opposed to only a single "no" vote (cast by Trent Lott against judge Roger Gregory, the first Black ever appointed to this position).
Bush appointed Joseph Allbaugh as head of FEMA in 2001, although Allbaugh had no expertise or experience handling emergencies, but rather had been then-Texas-Governor Bush's chief of staff & campaign manager for Bush-Cheney nationwide campaign. (Allbaugh had B.S. in political science from Oklahoma State University.) In 2003, Allbaugh replaced by Michael D. Brown – Former estate and family lawyer and bar examiner. The Boston Herald reports that Brown was "fired from his last private-sector job, overseeing horse shows... after a spate of lawsuits over alleged supervision failures... `He was asked to resign,' Bill Pennington, president of the IAHA at the time, confirmed last night."
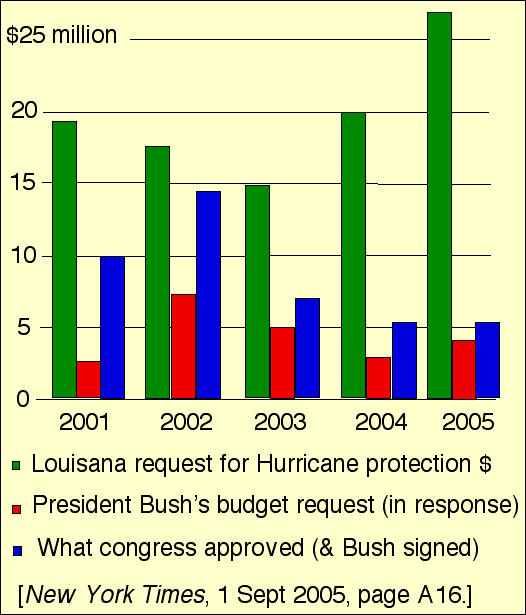
Pork & earmark game-playing:
FEMA (Federal Emergency Management Agency), in report well before both Hurricane Katrina and the 9/11 attack, summarized top 3 threats to the USA as a terrorist attack on New York, major earthquake in San Francisco and hurricane strike on New Orleans. But Bush and Congress by bipartisan budget vote turned down Louisiana's requests for mere tens of millions per year to protect New Orleans. New Orleans contained urban & poor people, many blacks, hence a high% Democrat voters; Louisiana had democrat senator, & starting in 2004, a democrat governor.
Compare with: $28 billion embassy (constructing in Iraq); $231 million for Alaska bridge between Gravina Island (population<50) & Ketchikan (pop. 8,000); Wyoming $31 million in anti-terrorism funding in 2003 (more per capita than any state).
|
Pseudo-election with real US voters (122 range & 656 approval) simultaneously with the 2004 presidential election (as exit poll). Note RV psychological drive for human honesty ⇒ "nursery effect" ⇒ RV far more likely than AV to encourage growth of small third parties ⇒ enabling escape from 2-party domination, media lapdogs, rubberstamped party hack agency heads & judges, etc. Third parties: suicidally foolish to support anything besides range voting.
More data: French Approval-Voting Study and French Range-Voting Study.
1992 US Pres. Election [analysis NES data by Steven J. Brams & Samuel Merrill III Politics and Political Science 27,1 (March 1994) 39-44], the vote totals again would have been tremendously altered with approval voting (although finish order would not have changed) again illustrating tremendous distortionary penalty faced by third-party candidates under plurality system.
And in the 1980 US Presidential Election, according to analysis based on many polls in ch. 9 of Brams & Fishburn's book,
| Candidate | Plur | AV |
|---|---|---|
| Clinton(Dem) | 43.0 | 55 |
| Bush(Rep) | 37.4 | 49 |
| Perot | 18.9 | 42 |
RV has some further advantages perhaps not mathematically explainable, but which instead are experimental facts that are consequences of human psychology:
| Plurality: 1.0-3.1% spoiled (6 countries). IRV: 3.4-6.2% spoiled (Australia 8 territories). |
| French 2002 approval study: 2.0% spoilage for official plurality votes, 0.3% for approval exit-poll votes. |
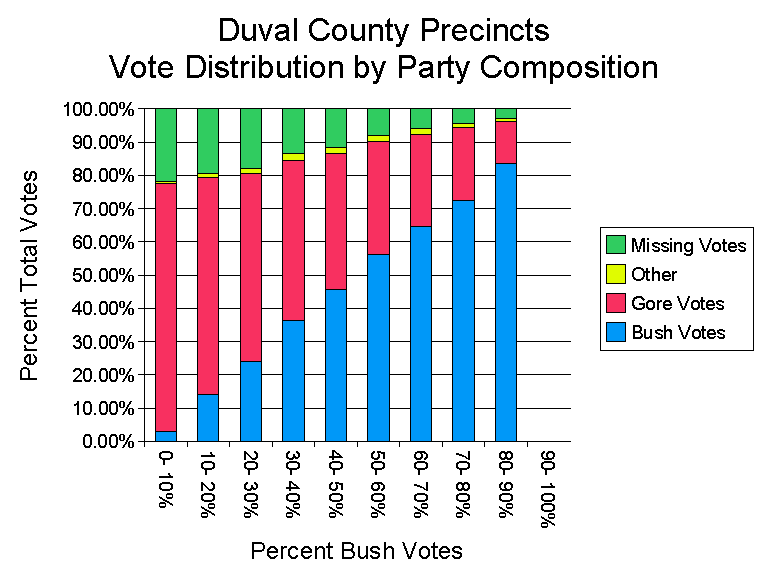
| County | Black pop. | Uncounted | – | County | Black pop. | Uncounted |
|---|---|---|---|---|---|---|
| Gadsden | 52% | 12% | – | Citrus | 2% | 1/2 % |
| Madison | 42% | 7% | – | Pasco | 2% | 3% |
| Hamilton | 39% | 9% | – | Santa Rasa | 4% | 1% |
| Jackson | 26% | 7% | – | Sarasota | 4% | 2% |
Cornell U. prof. Walter Mebane Jr. analysed ballot-level data from the NORC Florida ballots project and ballot-image files, concluded that "If the best type of vote tabulation system used in the state in 2000 – precinct-tabulated optical scan ballots – had been used statewide then [due to inequities in the distribution of voting machines & settings of those machines] Gore would have won by more than 30,000 votes." [ W.Mebane Jr.: The Wrong Man is President! Overvotes in the 2000 Presidential Election in Florida, Perspectives on Politics 2,3 (September 2004) 525-535]
This happening not only at the county level, but also district by district statewide. 268 Duval precincts: fluke result due to random fluctuations? Not. Enough to swing the Bush-Gore election result in Florida (which was decided by an official margin of only 537 votes)? Easily. (Palast maps, caption)
1. Range Voting works, simply, on every (plurality) voting machine!
Mathematically: ∃ transformation of one C-candidate (0-9 plus X) range voting election to 11C artificial "plurality elections." In some cases, this is easy and convenient from the viewpoint of voters (optical scan machines) in others it is less convenient (which is why we would prefer to have purpose-designed range-voting machines) – but it always works, easing transition worries greatly.
Demo:Award each candidate a numerical score from 0 to 9. Advise giving your favorite candidate 9 and the worst one 0. If you intentionally wish to express no opinion about that candidate, then please do not select any score for him – equivalently leave the default "X" choice selected; only numerical scores will be incorporated into the averaging.
Also try zohopolls, or this instant runoff demo (IRV will not run on many of today's voting machines).
2. Range Voting can get unified third-party support (due to Nursery effect, they'd be crazy to support anything else).
3. Range Voting reduces risk of tie & near-tie "chad counting lawsuit nightmare" scenarios (IRV increases risk)
4. Iowa primaries strategy:
| #candidates: | C=2 | 3 | 4 | 5 | 8 | 10 | 15 | 20 | 50 | 100 | 200 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5123 voters | 100% | 73% | 61% | 52% | 38% | 32% | 24% | 19% | 8% | 4% | 2% |


Honeybee (Apis Mellifera) swarms (each spring) and the 3mm-long eusocial ant Leptothorax Albipennis (after nest destruction) both use range voting to decide on the location of their new nest.
Problems bees face: Tiny brains. Can they do "addition," "division," and "averaging"? If so, can they communicate results reliably? What if some bees mentally defective or miscommunicate? How to reach a swarm-wide consensus? How to do it quickly? "Robust log-time parallel algorithm"...
How bees do it:
How good are they? Swarm: 2000-20000 bees. ≥1015 elections so far. Usually find ≈20 different housing options within about 100 km2, and ≈90% of the time, bee swarm succeeds in selecting (what appears to entomologists to be) best one.
Compare plurality-using humans: Computer sims ⇒ 1283 honest plurality-voters, given 10 choices (each voter regards each choice as worth standard-normal-random-number "dollar amount," all randoms generated independently before experiment begins) succeed in choosing the best (maximum ∑ dollars) 32% of the time.
Random guess: (10%),
Sim-humans employing "approval voting" (approving choices with value greater than midway between the best & worst available) then 54%.
Sim-humans employing "range voting" (scoring best choice 99, worst 0, rest linearly interpolated) then 79%... at least approaching bee-quality.
Ants: The most successful macroscopic land animals (15-20% of all land animal biomass?!). 200 Myr old.
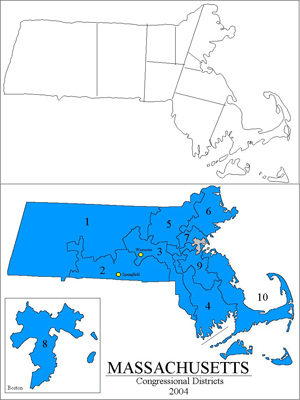 |
Shortest splitline algorithm eliminates gerrymandering. Basically: find shortest line splitting state into two parts with right population ratios, then continue recursively. This produces better district maps for less cost than present methods and is completely unbiased. Blue map shows Massachusetts as gerrymandered to have 100% Democratic congressmen, versus districts that would have been produced by splitline.
Arizona 2004 (pdf); Texas 2003 before & after (jpg); Art gallery (gifs); Illinois 2004 (pdf); (Chicago gifs); N Florida gifs; S Florida gifs+closeups; Maryland gif as redistricted. Splitlinings for all 50 states;