Non-integer solutions would be inconvenient because politicians do not like being cut in half. Hence for those problem versions we could end up having some other (i.e. not W) integer number of seats consistent with all the other (nonparenthesized) constraints. However in the unextended (or less extended) forms of our voting problem, the W-seat demand will be satisfied automatically, even without explicitly imposing it, just because, e.g, the sum of the demanded district-occupancies equals W if all Mk=Nk.
Dual form of our linear program
When we apply the linear programming duality theorem, we find our LP is equivalent to the following. (We'll assume Sj=Tj and Mk=Nk for this purpose.) Seek "additive adjustments" Uj≥0 for party j and Vk≥0 for district k such that
We then elect the Nk candidates in district k having
the maximum adjusted average score
Balinski's "fair majority voting" system, and its relationship (but inequivalence) to ours
Balinski's system begins by soliciting from each voter in each district a "name one candidate" plurality-style vote, saying their presumably-favorite candidate running within their district. Each such vote for a candidate also counts as a vote for his party. Balinski then determines each party's "deserved" seat count, by applying d'Hondt's method to the party vote counts. (Balinski prefers d'Hondt, while I prefer Sainte-Laguë, for this purpose. It perhaps is of interest that Germany's Bundestag originally used d'Hondt, but as of 2005 has switched to Sainte-Laguë.)
Then "multiplicative adjustments" ρj>0 for party j and λk>0 for district k, are found, such that if the vote counts are adjusted – i.e. any vote cast within district k is multiplied by λk and any vote cast for a party-j candidate is multiplied by ρj – then the winners in each district using adjusted votes, yield the deserved number of seats for each party.
So Balinski's system is the same as ours, except for the following changes:
- Balinski uses plurality-style ballots, while we use score-style.
-
Balinski uses d'Hondt, we use Sainte-Laguë. (Balinski claimed that was since he wanted the USA to
develop a "majority party" and d'Hondt made that more likely.
Evidently Balinski felt for some mysterious reason that
the USA did not already have enough 2-party domination.
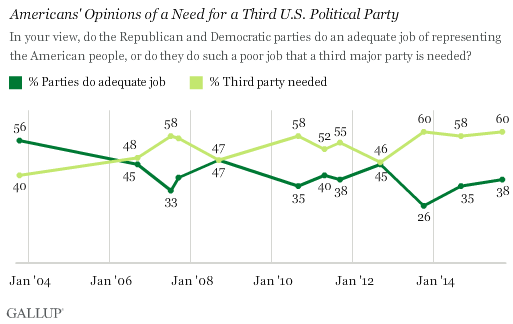
Polls of US citizens, however, disagree, with 60% finding the USA needs a third party.)
- Balinski uses multiplicative adjustments, while we use additive ones. (But Balinski's also are additive after logarithmically transforming everything, in which sense his and my methods are "the same.")
While I believe all three of these choices by Balinski were unwise, the last one was truly absurd, because...
What Balinski's LP is optimizing and why that was the wrong thing to optimize
We optimize the right thing, namely, the sum, over all MPs, of their average score reckoned by voters. This is the obvious naive approximation to the "quality" or "social utility" of the parliament, as estimated by voters. Balinski maximizes the sum, over all MPs, of the logarithm of their number of votes. (Equivalently, he maximizes the product of their vote-counts.) This has little relation to anything utilitarian.
How "targeted killing" strategic voting method would devastate Balinski's system and render it utterly unfit for direct use in designing the government of a country
With Balinski, the NaziLoon party (which gets 1% of the votes and hence deserves 1% of the seats) necessarily will enjoy a multiplicative scale-up factor of about 50, as compared with the Mainstream party (which gets 50% of the votes) with a multiplier of about 1. In other words, Balinski is going to force each NaziLoon vote to count about the same as 50 Mainstream votes.
This is a huge "leverage" or "amplification" factor subject to easy exploitation via "strategic voting." For example, suppose for the purposes of argument that Justin Trudeau (leader of Canada's Liberal party, recently elected prime minister in 2015) is the most popular MP in Canada. So the Tories might like it considerably if Trudeau's district were to un-elect him and thus remove him from power. Tory leadership can easily accomplish that goal. They simply tell the Tories in Trudeau's district "we suggest that instead of voting Tory, which is a lost cause, you vote NaziLoon." The 50× amplification factor then easily carries the day, and – voila – Trudeau is gone.
I call this "targeted killing." Now the Tories might now want to try that again, selecting as their target some other important Liberal MP. If, however, they kept re-using the NaziLoon party as their pawn in the targeted-killing game, it would no longer work as well. So instead, for their next "target" the Tories would switch to using the BeerLovers party as the (new) pawn. And so on.
This would cause all the important leaders in Canada to be "assassinated" – removed from political power – and instead a ragtag random collection of normally unelectable NaziLoons, BeerLovers, etc would be all over parliament. So perhaps the best two-word description of the situation that would be caused if Balinski's voting system were the design for Canada, would be "complete devastation."
The lesser (but probably still unacceptably severe) vulnerability of our system to "targeted killings"
With our system, which has additive rather than multiplicative adjustments to votes, the situation is somewhat less dire than with Balinski. There will no longer be a 50× amplification factor for NaziLoon votes which could be used to "kill" any "target." Instead, the NaziLoons will get a large additive "head start" in vote count in each district. Because Trudeau (in our example above) was postulated to be a very popular Liberal MP, it would still take a lot of NaziLoon votes to overcome him in his district, and it would be far easier and much more likely to work, to target an unpopular Liberal MP in this way. So it would no longer be possible to target essentially anybody. Only some targets, usually comparatively unattractive ones, would be easily "hittable."
Nevertheless, even with our system there would be some easily predictable places where easily-determined strategic voting could be used to hit hard. These hits would be highly effective and also would, as a side effect, distort PR to artificially enrich parliament with fringe candidates.
Why neither Balinski's nor our systems should be expected to "eliminate gerrymandering"
Balinski (judging by his title) seems to hold the view that with his voting method, gerrymandering will vanish because it is no longer useful. From then on, districts would be drawn sensibly, for a refreshing change!
Unfortunately, we believe Balinski is wrong about that. We think it quite likely, unfortunately, that gerrymandering would persist and continue to corrupt the USA massively.
Nationwide, we get proportionality, therefore it does not pay to gerrymander. Agreed. But locally, gerrymandering pays – plenty!
Suppose you are Joe Democrat Congressman. You'd like to have a safe seat. So you get your buddies in the statehouse to draw you a safe district full of Democrats.
Result (under Balinski voting): Joe is almost certain to be elected. The only way Joe can fail to be elected is if the entire country decides it hates Democrats hugely, and/or Joe's district stops voting Democratic – both of which are almost impossible. (Well, if we ignore the above about "targeted killings.")
So what I predict would happen (with Balinski voting) is this. The Democrats and Republicans will make interparty deals (just as they already do) to draw "safe" districts for all their high-ranking members. As usual, none of them will be defeatable.
But there will also be some districts occupied by lower-ranking Dems and Repubs, who do not have as much influence with the party bosses, which will be "at play." Those will be unsafe seats. So Balinski might improve things, but by no means will eliminate either gerrymandering or "congressmen for life."
Because of proportionality, the Greens will be able to get elected too. There could in principle actually be districts that are safe for Greens (i.e. essentially guaranteed to elect a Green). That is because the Greens will (by proportionality) win, say 5% (or whatever) of congress. The most-Green district in the country will then be essentially guaranteed to elect a Green, even though it (say) contains only 10% Greens.
Ivan Ryan comments: Locals might be pissed at a third-party which sets up its base in their district so it can consistently get 5% of the vote – the result being that 95% of the residents of the district are represented by a wacko-fringe party that they don't support.
Now the Dems and Repubs could (and probably will?) conspire to hurt the Greens as follows. Although the Dems and Repubs will be unable to prevent 10% Greens from being elected if the voters are 10% Green, they can keep shifting the Green district-boundaries with the goal of preventing any Green from being reelected. Or, they could try to make all the districts safe for everybody, so nobody ever gets defeated. This won't entirely work (if the country shifts from 60-40 R/D to 40-60, say, then there will be a 20% change) but it will work in the sense that all the established party members will be safe everywhere. Further, if, say, the Dems arrange to make their seatholders all have districts packed with Democratic voters, we don't see how that will hurt the Democratic party:
- Their seatholders will now be safe.
- The remaining parts of the country, which contain (say) only 1% Democratic voters because the gerrymanderers sucked it dry, still will elect Democrats because of the proportionality guarantee, so the party as a whole is not hurt.
So, sorry Balinski – there is huge incentive to continue to gerrymander. Indeed, the ultimate limit would be that every district is 100% politically monolithic. In that case, yes we'd get proportionality, but every congressman would be a congressman for life (the opposite of democracy) and the country would be totally divided+polarized into utterly predictable red and blue chunks.
Indeed, Balinski throughout his paper about "eliminating gerrymandering in the USA," appeared to be completely unfamiliar with the fact that a large number (probably "most") of the seats in the USA are "bipartisan gerrymandered" and indeed unaware even of the existence of the concept of "bipartisan gerrymandering." And also, with the fact the USA's districts are drawn, not federally, but rather locally (i.e. state by state). For next time, I would recommend Balinski acquaint himself with the basics about an area before he revolutionizes it.
Would it be acceptable to use our system merely as a "top up"? Yes, and the simple result is "MMP with score voting."
The idea would be: first to elect 1 MP per district in an old-fashioned (non-PR) manner, i.e. with single-winner elections within each district independently. (Preferably the score voting single-winner voting system would be used, not "first past the post.") Then we would add "top-up" MPs to try to bring the parliament back toward proportionality. (There would be some pre-specified number W of seats in parliament, of which W-T were single-MP-in-district seats and the remaining T were top-up seats.) The number of top-up seats from each party could be obtained using Sainte-Laguë based on each party's vote counts, but now starting the Sainte-Laguë seat-addition procedure not from zero initial seat-counts for each party, but rather from the party seat-counts arising from the initial W-T "one MP per district" elections.
Sainte-Laguë seat-addition procedure: Let Vj denote the vote-count for party j, and Sj denote its current seat count. Find the party with the greatest V/(2S+1) value. Give that party one additional seat (incrementing its S). Keep doing this, one seat at a time, until all the seats in parliament have been labeled with party-occupancy labels. [d'Hondt is the same except that the formula V/(2S+1) is replaced by V/(S+1).]
With each party's deserved-seat count known for the top-up seats, the plan then would be to employ the linear program here to choose the T top-up MPs optimally while meeting the party-occupancy demands. This task would, in fact, be trivially simple, i.e, no linear programming would be needed! That it because we simply would, for a party deserving S more seats, simply elect the S highest-scoring as-yet-unelected MPs from that party. This essentially would be the (already well known and already used, e.g. in Sweden) Sainte-Laguë method of "party lists" but used as a top-up method, with the list ordering within each party simply being descending order by average scores received by their candidates from the voters in their districts.
If we wanted to impose the additional demand that no district could have more than one top-up MP, though, then we would need linear programming, and indeed integer programming. The latter might be too computationally difficult for feasibility. Linear programming is computationally efficient. Integer programming is not and too-large integer programs can be infeasible to solve. (Anyhow quite likely such an integer-programming-based top up would not even be desirable, if the "targeted killing" threat were considered worse than the problem of occasionally having districts with several MPs.)
Here is a list of advantages and disadvantages of the resulting system:
- Pro: Very simple, well known, method with historical experience of use (approximates the "MMP" systems currently used in Germany and New Zealand) with no linear or integer programming needed.
-
Con: needs explicit use of party names. "Independent" candidates, therefore, are placed at a severe disadvantage,
or anyhow treated unequally. It is probably not a good thing if a country, by law, in the
definition of its voting system itself, disparages or forbids independent thinking. In the USA during 1970-2015,
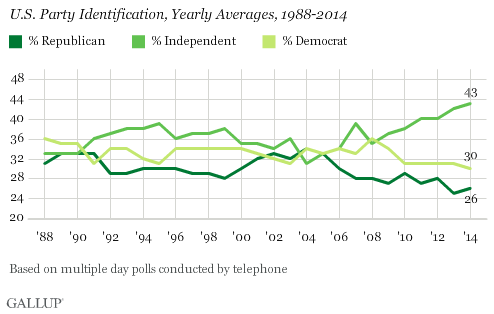
approximately 1/3 of voters identified themselves as "Democratic," approximately 1/3 "Republican" and
approximately 1/3 Independent. In 2015, Gallup reported that the precise count was
43% Independent, 30% Democrat, 26% Republican:
At the same time, Ipsos (on behalf of Global News) polled Canadians about how they would vote (if they could) in the USA presidential election, finding 55% Democrat, 28% Independent, 17% Republican. In Hong Kong, the majority of the legislative council consists of independents. The Irish Dail (elected via a PR system defined in a way that nowhere mentions "parties") contained 10% independent MPs during 2011-2015. This contrasts with Poland, which had zero, since the Polish system basically makes it impossible to be an independent politician. Many countries over time have experienced a rise in party control, which has caused a decrease in the numbers of their independent politicians. In the opinion of many, this trend has been bad. So if we were to use the present section's "proportional representation" party-list top-up system to elect a parliament, and if it resulted in fewer than 1% of MPs being independents (duplicating Canada's 2015 situation) – then that wouldn't be "proportional representation." It would be "an enormous distortion of PR." - Think that's unrealistic? The two most prominent countries using an MMP system to elect their parliaments are Germany (Bundestag) and New Zealand. In the German Bundestag's first election in 1949, three MPs were independents. In all elections after than (up to 2015) there have been zero. New Zealand installed its current MMP system in 1996. The last independent MP elected was Winston Peters (elected in 1993); up to 2015 there have been no others. It is possible to repair this perceived problem to some extent by regarding all the independents as a pseudo-party (the "independents' party"). Of course, many independents are quite dissimilar, so that such an agglomeration could be highly misleading. But from the standpoint of just providing an extra boost to independents versus party candidates to try to repair inherent pro-party unfair biases, this repair ought to work pretty well.
- Con: it is possible to "game the system" tremendously by switching party affiliations. To stop that, New Zealand (which uses a top-up system of a similar nature) found it necessary to enact anti-switching laws making it illegal for politicians to switch parties. Such laws are not exactly conducive to independent thinking. (I am writing this in 2015. New Zealand has not had any Independent MPs for over 20 years.)
- Con: the top-up MPs are "countrywide" and not "regional," and since some districts will have more than one MP due to top-ups, that could be viewed as unfair. It is possible to repair this perceived problem to some extent by dividing the country into, say, 20 regions, and electing 1/20 of the parliament from each region (complete with its own top-ups and own party-lists inside each region). The regions conduct elections independently using the top-up system we've described (each region contains many districts inside) and then at the end all the regional subparliaments are merged to obtain the full countrywide parliament.
- Con: In this kind of system, it can be strategic for voters not to vote for their favorite candidate. Such votes can be "wasted" and it can be strategically better to lie so that you can elect a "lesser evil."
References
Michel Balinski: Fair Majority Voting (or how to eliminate gerrymandering), American Mathematical Monthly 115,2 (Feb. 2008) 97-113.
Steven J. Brams & Peter C. Fishburn: Proportional representation in variable-size legislatures, Social Choice and Welfare 1,3 (Oct. 1984) 211-229.
George B. Dantzig: Linear programming and extensions, Princeton Univ. Press 1963.
A.J.Hoffman & David Gale: Appendix within the paper I.Heller & C.B.Tompkins: An Extension of a Theorem of Dantzig's, pp.247-254 in H.W.Kuhn & A.W.Tucker eds. Linear Inequalities and Related Systems, Annals of Mathematics Studies #38, Princeton University Press 1956.