[Brookings Institution Policy brief #88, 2000]
ABSTRACT:
The dramatic changes in state populations revealed by the 2000 census will cause twelve seats to shift from one state to another in the House of Representatives in 2002. Although much attention is being devoted to redistricting within states, not enough is being paid to a fundamental flaw in the formula used to allocate the 435 seats among the states. This peculiar method, first adopted in 1941, violates the principle of one person, one vote by systematically giving more representation to residents of small states than to residents of large states.
Fortunately, the situation is easy to fix: a simpler formula, first proposed by Senator Daniel Webster in the 1830s and currently used in other representative democracies, treats small and large states even-handedly. Reinstating Webster's method now – well in advance of the next census – will restore the long-term balance between small and large states.
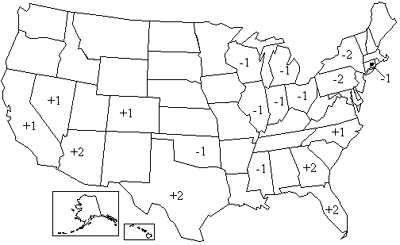
Every ten years, a new census leads to a constitutionally mandated reapportionment of the House of Representatives. Inevitably, this process has major political consequences, and the 2000 census is no exception. The new apportionment will cost the Northeastern states ten seats and give a substantial boost to the political fortunes of the South and the Southwest, as shown in figure 1.
Unfortunately, the process that governs reapportionment is fundamentally flawed. Through a strange combination of historical accident and political and mathematical intrigue, Congress is presently saddled with one of the most peculiar apportionment methods used anywhere in the world. Not only is it unnecessarily complex – involving square root formulas – it demonstrably favors small states at the expense of large states. Fortunately, there is an easy way to remedy the problem, as I will explain here.
A number of political factors have converged to make the issue of equal representation particularly potent this year. There was extensive debate in the executive and legislative branches leading up to the 2000 census about how to correct for errors that tend to undercount minorities. Then there was the contested presidential election, which made Americans keenly aware that every vote really does count. Finally, there are questions of fairness in how district lines are being redrawn within the states.
These issues have fed public concern that the right to equal representation is perhaps being compromised. Given these perceptions, Congress would do well to reform the inequitable process by which seats are distributed among the states in the first place. Although Congress can take up this matter at any time, this seems like a particularly propitious moment, since it could correct a long-term problem in the system with no short-term political consequences, because no seats would shift this time around.
How could such a seemingly straightforward problem turn into such a quagmire? In particular, why not simply take each state's fraction of the total population, multiply it by the total number of seats (currently 435) to determine each state's seat quota (see figure 4), and then round the quotas to the nearest whole numbers?
To illustrate the difficulty, consider the example in figure 2 [below], which represents a hypothetical federation of three states with a "house" of 21 representatives: inspection of the quotas shows that ordinary rounding will not work because all three states would be rounded down, and thus only 20 seats would be apportioned.
The earliest proposed solution to this difficulty came from Alexander Hamilton in 1792, who suggested rounding the quotas in the usual way, and if any seats are left over, giving them to the states with largest remainders. In figure 2, state B, with remainder .41, would receive three seats under Hamilton's method.
| Figure 2 | |||||
|---|---|---|---|---|---|
| State | Population | Quota | Hamilton | Quotient(480,000) | Jefferson |
| A | 7,270,000 | 14.24 | 14 | 15.15 | 15 |
| B | 1,230,000 | 2.41 | 3 | 2.56 | 2 |
| C | 2,220,000 | 4.35 | 4 | 4.63 | 4 |
| Totals | 10,720,000 | 21.00 | 21 | 22.34 | 21 |
| Source: author's calculations | |||||
While that approach may seem straightforward, later experience would show that it was fraught with difficulties. At the time, Hamilton's nemesis, Thomas Jefferson, argued that the method was fundamentally wrong. Jefferson asserted that the correct approach was to choose a common divisor, divide it into each state's population, and drop the fractional part of the resulting quotient. The "trick" is to adjust the divisor so that the required number of seats is apportioned.
Jefferson's approach apportions each House size in an essentially unique way, because as the divisor is adjusted downwards (or upwards), exactly one state at a time gains (or loses) a seat, barring improbable ties.
In the 1790s debate, Jefferson prevailed over Hamilton – not because Congress recognized its mathematical subtlety, but largely because it gave one more seat to Virginia, which at that time was the most populous and most politically important state. Jefferson's method was used through the 1830s, even as it came under increasingly bitter attack in Congress because it blatantly favored large states. (If Jefferson's method were in use today it would give California 55 seats, even though California's current seat quota is only 52.45.)
The evident bias of Jefferson's reapportionment method ultimately led to its abandonment in 1840, when it was replaced by a method first proposed in 1832 by the brilliant orator Daniel Webster. Like Jefferson, Webster began with a common divisor, but instead of dropping the fractional remainder, he argued that fractions should be treated in the usual way: rounded up if the fraction was more than one-half, rounded down if it was less. As with Jefferson's method, there typically exists a range of divisors that apportions the required number of seats and does so in a unique way.
Webster and Hamilton's methods were used sporadically until 1900, when Webster's approach definitively replaced Hamilton's. The reason for rejecting Hamilton's method was its bizarre behavior when the size of the House changed. In the 1880s, for example, an increase in the House size from 299 to 300 seats would have caused Alabama's allotment to decrease from eight seats to seven.
To see how this can happen, consider the hypothetical three-state example described in figure 2 and suppose that the House size were increased from 21 to 22 seats. The quotas would be as follows: state A, 14.92; state B, 2.52; state C, 4.56. To apportion 22 seats, Hamilton's method would round two states up and one down (even though all remainders exceed 0.5). Since the state with the smallest remainder is B, it must be the one rounded down. In other words, in a 22-seat House, state B receives only two seats, whereas in a 21-seat House, it would receive three seats. This absurdity was dubbed the "Alabama paradox" and led Congress to abandon Hamilton's method – thus showing that intuitive mathematical principles can, at least occasionally, play a role in politics.
It could be argued that, since the size of the U.S. House of Representatives is currently fixed at 435, the Alabama paradox is no longer relevant. But Hamilton's method also displays unacceptable behavior when the House size is fixed and the state populations change. In particular, a state with an expanding population can lose seats to a state with a declining population, a phenomenon known as the "population paradox." For both of these reasons, Hamilton's method must be deemed unacceptable.
But are there any more reliable methods? In fact, there is a large class of methods, of which Jefferson's and Webster's are particular examples, that avoid both paradoxes. All of them are based on the principle of the common divisor invented by Jefferson.
Using this method, each state population is divided by an adjustable divisor to obtain a quotient. The quotients are then rounded to whole numbers and one adjusts the divisor until the rounded numbers add up to the required number of seats. Any such rule is called a divisor method; the only issue is how to round the quotients to whole numbers. Webster's method – rounding each quotient to the nearest whole number – is the most logical.
In addition to the methods of Jefferson and Webster, three other divisor methods have been proposed over the course of U.S. history. John Quincy Adams argued in 1832 that all quotients should be rounded up instead of down, no matter how small their fractional parts. Conveniently, this would have saved a couple of seats for New England, his constituency. The same year, James Dean, a former professor of Webster's at Dartmouth, suggested a complicated method that entailed rounding up the quotient if it exceeds the harmonic mean of the two nearest whole numbers. Otherwise, he said it should be rounded down. (The harmonic mean of two numbers is their product divided by their average. So if a quotient is 2.45, it should be rounded up because it is more than 6 (the product of 2 and 3) divided by 2.5 (the average of 2 and 3).
Joseph Hill, a Census Bureau statistician, suggested an equally bizarre alternative in 1911 that was later refined by Harvard mathematician Edward Huntington, and which the House uses to apportion seats today. They argued that a quotient should be rounded up if it exceeds the geometric mean (or square root of the product) of the two nearest whole numbers. Using this method, a quotient of 2.45 would yield three seats. (The square root of 2x3=6 is 2.449 which is less than 2.450.)
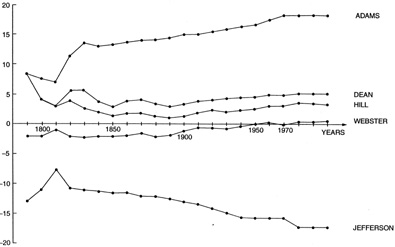
The 50-state chart gives the 2000 apportionments by each of these five divisor methods (and also by Hamilton's method). An inspection of the table reveals an interesting pattern. Arranged in the order Adams, Dean, Hill, Webster, Jefferson, each divisor method progressively favors large states more and small states less. For example, Adams's method would give South Dakota, whose seat quota is 1.170, two seats.
From a policy standpoint, the crucial question is whether any of these methods treats small and large states even-handedly over a period of years. (Hamilton's method is even-handed, but it has proven to be so prone to paradox that Congress would likely never revert to it.) To examine this issue empirically, we can review the solutions that each of these methods would have given if they had been used from 1790-2000 (see figure 3).
To account for the constitutional mandate that each state, no matter how small, must get at least one seat, I omit the very small states with a quota of less than one-half in order to examine whether any bias remains after deleting these "very small" states.

The remaining states are then divided into three categories – large, middle, and small – with the middle category taking up the slack if the number of states is not divisible by three. For each method and each census year, I compute the per capita representation in the large states as a group and in the small states as a group. The percentage difference between the two is the method's relative bias toward small states in that year. To estimate their long-run behavior, I compute the average bias of each method up to that point in time.
The results are shown in figure 3. Only Webster's is close to being unbiased, while the method currently in place (Hill's) systematically favors the small states by 3-4 percent.
Given these findings, it is remarkable that the current method was adopted. That happened in part because some of the country's leading mathematicians – including John von Neumann, Marston Morse, and Luther Eisenhart – claimed that it was unbiased. In a National Academy of Sciences report to Congress, they claimed that Hill's method was preferable because it "stands in a middle position as compared with the other methods." In other words, the mathematicians argued that two methods favor small states more than Hill's method does, and two methods favor small states less. Using this reasoning, it was fortunate for them that Congress was considering an odd number of methods. Empirical evidence that was not considered by the mathematicians – such as the actual effect of different methods over the course of United States history – shows that on the contrary, Hill's method is biased and Webster's is not.
Of course, politics also played a role in the outcome, as it always has: the switch from Webster's to Hill's method in 1941 gave one more seat to Arkansas and one less to Michigan, which essentially guaranteed one more seat for the Democrats (the majority party). It is also true, however, that the scientific arguments bolstered the Democrats' case.
Indeed, apportionment debates over the years exhibit an interplay between political and mathematical logic. Jefferson's method was ultimately rejected because of large-state bias, Hamilton's because of bizarre behavior when the House size grew. Changes in method had to wait, however, for the underlying problem to be articulated and for the congressional votes to be in place.
The current dilemma is clear – Joseph Hill's method favors small states over large ones. If Congress begins the task of changing the apportionment formula now, it will avoid a more complicated political fight when the next census rolls around. With Webster's method reinstated, the treatment of large states and small states will be brought into better balance and in the long run, all states will be fairly represented.
This Policy Brief is based on a new book, Fair Representation: Meeting the Ideal of One Person, One Vote (2nd edition) by M.L. Balinski and H. Peyton Young, published this year by the Brookings Institution.
The Brookings Institution, 1775 Massachusetts Ave NW, Washington DC 20036
Telephone: (202) 797-6004
E-mail:
Brookings Info or
Comments on This Site