Donald G. Saari is a mathematician. Remarkably, "Saari favors a [voting] method called the Borda count." (That was a quote from Dana Mackenzie [Discover Magazine November 2000].) I say "remarkably" because Saari is almost the only voting expert in the world who doesn't think Borda is a very bad voting method. But Saari is a rather prolific and publicity-hungry one, and thus, unfortunately, has an outsized impact on the popular mind.
Borda is worse than range voting in every way I can think of: less expressive, worse for honest voters, worse for strategic voters, extremely sensitive to voter-strategy, vulnerable to candidate cloning, more complicated both for the voter and for voting machines, severely fails irrelevant alternatives, and incentivizes "favorite-betrayal."
So what underlies Saari's view? We now go though various public statements by Saari, showing how they are wrong, miss the point, and/or work at least as well (or better) as a pro-range-voting argument than as a pro-Borda argument. We conclude at the end by showing there was one unified wrongheaded theme in all Saari's work.
Dana Mackenzie, SIAM News (21 October 2000) article on Don Saari's voting accomplishments: "According to Saari's analysis... If you think that the outcome for a profile with cyclic symmetry should be a tie (and everyone questioned by Saari has replied that it should), then you should choose a voting method based on rankings – in any such system, the candidates in a cyclic profile have the same number of firsts, seconds, and so forth. If you believe that the result for a profile with reversal symmetry should be a tie, then you should choose a voting method based on pairwise comparisons, like Condorcet's criterion. And if you think both of the above profiles should be ties? In that case you have one choice; the only voting method that can be expressed both as a ranking method and as a pairwise-competition method: the Borda count. Saari's proof of this fact is a tour de force of linear algebra..."
Saari again saying the same thing (Dana Mackenzie, Discover Magazine Nov 2000): "The reason voting procedures give us paradoxes and unwanted outcomes is that they do not respect the symmetries of data that give us ties," Saari says. Is there any system that would consistently declare the vote of Alice, Betty, and Cheryl a tie, and would do the same for Andrew and Bob? "Only one procedure does that," Saari says. "The Borda count." To prove his point, he published two 50-page papers on the Borda count in the January 2000 issue of the journal Economic Theory. END QUOTE.
Our response: Borda is the "only" such voting method? Wrong. Range voting is another. (Reversal symmetry for [0,1] range voting: x→1-x.) Saari's "proof" simply began by defining range voting as "not" a voting method at all, then proceeded to prove that Borda was the only voting method satisfying his criteria. It is easy to "prove" things by methods of that nature. For example, if I want to prove 1+1=5, I begin by defining 1 "not to be" a number. More precisely, Saari in this and other works, only considers the class of "weighted positional" voting systems, which is a tiny subclass of "rank order ballot" voting systems, which is a tiny subclass of all voting systems. Any results by Saari that Borda is the "best" voting system, or the "only" voting system with some property, mean, therefore, almost nothing. They are kind of like "proving" that milk is the "only" white substance, or the "whitest" substance, by as your first step declaring "we shall only consider liquid edible substances available at Shop-Rite."
Also, Schulze's beatpath Condorcet voting method is based on rank-order ballots, obeys reversal symmetry, and declares an exactly-symmetric cycle to be a tie. Oh gee. I guess that wasn't a "voting method" either.
In a recorded lecture distributed by the American Mathematical Society, Saari remarks that "lost information" is a top culprit behind lots of voting problems. For example if we ignore everything in a set of Borda votes except for the top rankings (i.e. we use plurality voting) that loses information. And that's terrible.
What Saari fails to remark (not only in this lecture, but indeed in all his published work so far): if we eliminate from a set of range votes, all strength information, we get Borda-style votes. So Saari's view is that losing information is terrible – except when that discussion makes Borda voting look bad, in which case he ignores it.
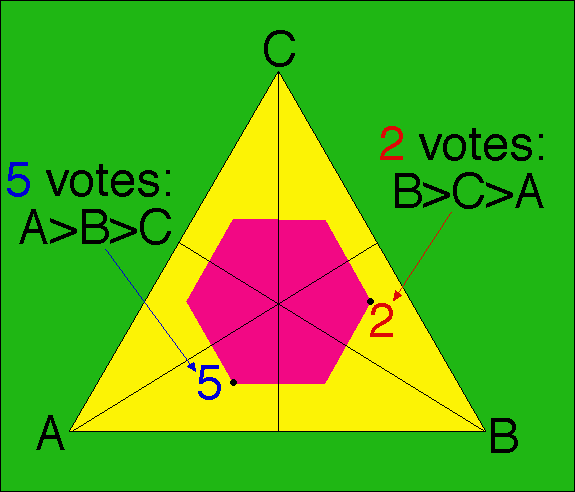
Saari has a pretty picture of 3-candidate Borda voting using an equilateral triangle ABC. You divide it into 6 congruent sub-triangles using angle bisectors. In each sub-triangle you write a number of votes. For example, if there are 5 "A>B>C" votes you write "5" in the subtriangle nearest to A and second-nearest to B. Borda voting consists then in just finding out where the "center of (numerical) mass" lies.
Nice picture.
Now with range voting, not all "A>B>C" votes are identical; some express greater strengths for some preferences. That corresponds, in fact, to placing a point in the cube [0,1]3, located at coordinates (a,b,c). If you look along the 1,1,1 direction then you see a two-dimensional picture of this, which is how Saari got his 2D picture. We can do that for range voting too; then a range vote is a point at (a-μ, b-μ, c-μ), where μ=(a+b+c)/3. This lies in the projection-plane X+Y+Z=0. Then range voting again just takes the center of mass to find out who won the election. We can do this all inside the 2D plane. Saari's set of possible Borda votes is 6 points forming the corners of a regular hexagon (shown pink). In contrast, the set of possible range votes is a solid regular hexagon, i.e. including the whole interior, not just its 6 isolated corners. (If you look at a cube along its diagonal, you see a regular hexagon as its silhouette.)
So with range voting we get a just-as-nice geometrical interpretation, with exactly the same symmetries. Saari forgot to mention that.
The top criticism of Borda voting is its horrible reaction to strategic voters. Borda himself is reported to have cried in frustration that his voting system was "designed for honest men."
To make this clearer: given that A and B are the two "frontrunners" most-likely to win, you are "wasting" some portion of your Borda vote if you do anything other than ranking them "top" and "bottom." In particular in a 12-candidate field if you (honestly) rate them top and 2nd-top, then you are a strategic idiot with over 10× less voting power than such an exaggerator. But if you decide not to waste over 90% of your vote, then you are being extremely dishonest about B, misordering him with respect to every candidate other than A. (And you have no choice about that because the rules of the Borda system force all that misordering. It's the same "fool versus idiot" choice you get with the "lesser evil dilemma" of plain plurality voting, writ larger.) So Borda incentivizes massive voter dishonesty, often resulting in extremely bad election results. In contrast, with range voting, a strategic AB-exaggerator would not be forced to misorder B with respect to anybody and thus would produce a far-more-honest vote without "wasting" any power. The change in rules from Borda to range voting thus may seem minor, but it has a far-reaching effect as far as its interaction with strategic voters is concerned.
When asked about this by William Poundstone (quoted in his 2008 book Gaming the Vote), Saari explained that the reaction of a voting system to honest voters has to be pre-eminent in our considerations, while the reaction to strategic voters must be secondary.
But how did Saari know that? Maybe strategic voters are more important. This is simply an opinion by Saari with no justification offered. And in the field of voting (as Saari himself repeatedly explains throughout his works) intuition is a poor guide.
How can we look at this more objectively? Several ways:
Hypothetical USA 2000 election using Borda (this quoted from Mackenzie's 2000 Discover article on Saari): How would McCain, Bush, and Gore have fared in a general election under the Borda count? The Sacramento Bee poll, plus the official tallies for California's open primary, offers a clue. According to the Bee's results, McCain would have beaten Gore 48 to 43, and Gore would have beaten Bush 51 to 43. But could McCain have beaten Bush among all voters, not just Republicans? Here's one way to figure it out. In the California primary, 60 percent of Republicans voted for Bush and 35 percent voted for McCain. We can assume that those percentages would have stayed the same had they been slated to run against each other in November. On the Democratic side, nearly 800,000 voters broke party ranks in March's primary to vote for Republicans. Of these, 64 percent voted for McCain and 31 percent voted for Bush. Again, the simplest thing to do is assume that the entire Democratic party would have split the same way if they were forced to choose between those two candidates in November.
So in our hypothetical Bush-McCain race, Bush would win by 60 to 35 among the Republican voters, and McCain would win by 64 to 31 among the Democratic voters. Overall, McCain would beat Bush, 50 percent to 45 percent. (To arrive at those figures I first added together each candidate's percentage of the Democratic and Republican vote [60 and 31 for Bush, 64 and 35 for McCain] and divided by 2.) To see how all three candidates would do under the Borda count, we add up the results of the head-to-head matchups:
| Gore=51 | Bush=43 | |||
| Gore=43 | McCain=48 | |||
| Bush=45 | McCain=50 | |||
|
|
||||
| Gore=94 | Bush=88 | |||
Hence, in California at least, McCain would have been the Borda count winner. END QUOTE.
Hypothetical France 2007 election using Borda: Essentially the same kind of calculation, with the same error, was done by Prof. Bruce P. Conrad [Jan. 2008 essay "How should we count the votes" on the American Math'l Society web site], now concerning the 2007 French Presidential election. Officially, the top 3 finishers in this election were Sarkozy, Royal, and Bayrou, in that descending order. Conrad knew the official Sarkozy:Royal runoff was won 53-47 by Sarkozy. He also knew from IFOP polls about hypothetical 2-candidate runoffs that Bayrou would have beaten Sarkozy 55-45 and Royal 58-42. Hence he concluded Bayrou would have won if France had run its election using Borda count:
| Sarkozy=53 | Royal=43 | |||
| Sarkozy=45 | Bayrou=55 | |||
| Royal=42 | Bayrou=58 | |||
|
|
||||
| Sarkozy=98 | Royal=89 | |||
What's wrong with both those calculations? The problem was there were not just 3 candidates. In France 2007 there were 12 candidates. Voting "A>B>C" giving A,B,C Borda scores 2,1,0 is not realistic. Really it'd be (say) this vote "A>x>y>q>z>m>r>s>t>B>u>C" giving them 11,2,0. Or something else. It all depends how the voters rate the other 9 candidates. Those other 9 candidates are not a "minor neglectible" effect. They are "the dominant" effect. A voter who ranks Sarkozy, Bayrou, and Royal at the top of her ballot (the way Conrad supposes) is about 10 times less powerful than one who ranks one top and another bottom. The effect of the 10× more powerful voters swamps out the wimpy voters Conrad was considering. Hence, Conrad's conclusion that Bayrou would have been the Borda winner is unjustifiable. (Perhaps right, but not justifiable.)
So who would have been the Borda winner? Nobody knows. But I can guess. My guess is that the Royal supporters would have ranked Royal top with both her major rivals ranked bottom. That is because they would not have wanted to be 10× less powerful. (Royal would have urged her voters to be "powerful" on her behalf. Not "idiotic" on her behalf.) Similarly the Sarkozy voters would have ranked Sarkozy top with both his major rivals bottom. Finally, the Bayrou voters would have ranked Bayrou top with both his major perceived rivals bottom. And yes, there would have been some voters ranking all three top, but their effect on the election would have been comparatively about 10 times smaller per capita. If we suppose neglectibly smaller, then we can prove this conclusion: Neither Sarkozy, Bayrou, or Royal would have won with Borda voting, because all three would have had below-average Borda score!
In fact this is exactly what happened in my only personal experience with a high-stakes Borda vote (and a similar experience was reported by Salvador Barbera) and another example occurred in the only government known to have employed Borda voting, Kiribati. Also, note in France 2002 under the same postulated voter behavior, none of the Big Three would have been a "Condorcet Winner," although based on those polls Bayrou was a Condorcet winner with honest voting. Bayrou was the range voting winner, which is a good illustration of the counterintuitive fact that range voting actually can be more likely to elect Condorcet winners than Condorcet voting methods!
I repeat: I do not know whether this (all three losing with Borda) would have happened. It is just my guess. But I think you can now see it is at least a plausible guess.
This actually is an excellent illustration of two well-known major flaws – clone vulnerability and vulnerability to inserting and removing candidates – in Borda voting.
This kind of strategic voter exaggeration also would be highly impactful with range voting, but range voting, unlike Borda and Condorcet, would not have caused a "dark horse" to win. One of the Big Three still would have won. And in fact we have a pretty good guess who, because a range-voting exit poll was conducted, and Bayrou won it.
Saari in an April 2008 Radio Interview (I have an audio recording) claimed that had either approval voting or range voting been used in the Bush v. Clinton v. Perot US presidential election (1992), then Perot would have won. Saari then indicated this was crazy because clearly Perot was bad and/or unwanted by the USA. This in Saari's view was a big flaw in Approval Voting.
But polls say Saari was wrong: In fact, nationwide approval voting polls were done for this election by two polling organizations (Gallup and New York Times) independently! And a range voting poll was also done! Saari didn't mention all that. The combined poll results show Clinton would have won with both approval and range voting (and Clinton also won with the official plurality voting system). Here is the data:
Approval voting: We combine this New York Times telephone poll of 1854 US citizens (on 23 Oct. 1992) "Is your opinion of Ross Perot favorable, not favorable, undecided, or haven't you heard enough about him yet to have an opinion?" (same question also asked for Bush & Clinton) with the result of an independent Gallup telephone poll of 1579 US citizens (on 31 Oct. 1992) [almost identical question phrasing except "undecided" and "don't know" lumped into one]. The results (for all 3433 pollees; note some rows may not sum to exactly 100% due to integer twice-roundoff effects) are as follows:
| Candidate | Favorable | Unfavorable | No opinion | F/U Ratio |
|---|---|---|---|---|
| H.Ross Perot | 36.4% | 39.4% | 23.7% | 0.924 |
| G.H.W.Bush | 39.6% | 47.8% | 13.1% | 0.828 |
| William J. Clinton | 40.8% | 42.2% | 17.0% | 0.969 |
Interestingly, note that no candidate got more "favorables" than "unfavorables." An academic paper by S.J.Brams and S.Merrill "Would Ross Perot have won the 1992 presidential election under approval voting?" PS: Political Science & Politics 27,1 (March 1994) 39-44 (pdf) also independently concluded, this time based on NES "thermometer" data, that Clinton would have won: they estimated Clinton 55%, Bush 49%, and Perot 42% approval.
Range Voting: (Market Facts Inc. telephone poll of 1000 US citizens on 18 Oct. 1992) "First I'd like to know how you feel about some of the presidential candidates. Use a 7 point scale where 7 means that you have an 'extremely favorable' impression, 1 means 'extremely unfavorable' and 4 means 'neither favorable nor unfavorable.' Of course, you can use any number between 1 and 7. How do you feel about Ross Perot?"
| H. Ross PEROT | 1 | 2 | 3 | 4 | 5 | 6 | 7 | (don't know/refuse) |
|---|---|---|---|---|---|---|---|---|
| avg=3.55 | 20.7% | 9.0% | 12.5% | 25.5% | 13.7% | 7.4% | 6.9% | 2.5% |
| Geo. H.W. BUSH | 1 | 2 | 3 | 4 | 5 | 6 | 7 | (don't know/refuse) |
|---|---|---|---|---|---|---|---|---|
| avg=3.58 | 25.2% | 9.4% | 10.3% | 19.2% | 13.1% | 8.4% | 11.7% | 2.0% |
| Wm.J. CLINTON | 1 | 2 | 3 | 4 | 5 | 6 | 7 | (don't know/refuse) |
|---|---|---|---|---|---|---|---|---|
| avg=4.08 | 19.0% | 7.3% | 10.1% | 15.9% | 14.2% | 14.3% | 15.7% | 0.0% |
| #Voters | Their votes |
|---|---|
| 3 | A>B>C |
| 2 | B>C>A |
| 2 | C>A>B |
So by Saari's very own "optimality" criterion, range voting is better than Borda voting.
But Saari did not mention that. (And his "proof" began by defining Range Voting "not to be" a voting system.)
Incidentally, another interesting analysis [Davide P. Cervone, Wm. V. Gehrlein, Wm. S. Zwicker: Which scoring rule maximizes Condorcet Efficiency?, Theory & Decision 58 (2005) 145-185] asks which WPV system maximizes the chance of electing a "Condorcet winner." Surprisingly (and contrary to a previous wrong article) the answer is not the Borda count. See puzzle #88.
One might, therefore, by analogy, speculate that some other voting system than range voting – specifically, involving some monotonic but nonlinear pre-transformation of vote-scores – would be better than plain range voting by this measure (with some utility-generator probabilistic model). However, that does not happen because with range voting any voter is free to perform any such transformation already. Thus plain range voting, if all voters "honestly and altruistically" decided to behave that way, would automatically maximize this (or any other) quality measure over the whole space of transformations. (This remark would, presumably, actually yield even better range voting "Bayesian regret" scores for honest voters than the ones measured, which already were better than all common-rival voting systems.) Meanwhile with Borda, voters cannot effectively "change the rules" in this way; they are stuck with Borda weights.
Saari has his own version of Arrow's Impossibility Theorem, and a way to redo it so that Borda is the only voting system the (revised) conditions allow. We now explain that and explain why it is stupid.
Here's Saari's wording of Arrow's theorem:
THEOREM (Arrow): If #candidates≥3 and #voters≥2 then any voting system obeying all these conditions must be a "dictatorship" (meaning a single voter, the "dictator," exists who has the power to decide who wins regardless of what the other voters do).
Saari then considers replacing assumption #3a with his alternative SAARI-ASSUMPTION-3a: The societal ranking of any pair A,B is determined solely by how the voters rank that pair and by the number of candidates they rank between A,B.
CONCLUSION (Saari): With this revision, Borda voting obeys all the conditions, and if a few extra assumptions also are added (the "anonymity" assumption that all voters are equivalent, is one; he says the others are "technical") Saari concludes Borda is the only voting system satisfying these assumptions.
Why this is stupid: Saari is specifically artificially constructing his axiom to get Borda out, rather than constructing reasonable axioms and then seeing what results. His SAARI-ASSUMPTION-3a is preposterous because it is not something we want a voting system to obey, it is something we want a voting system to disobey! Several papers have been written about how immunity to candidate cloning is a desirable property of a voting system. But here Saari is specifically demanding that the voting system be vulnerable to cloning, unlike the previous authors who (more reasonably!) had demanded exactly the opposite.
In other words, Saari just proved Borda is a uniquely bad voting system. But he then failed to cite or mention all of the previous anti-clone authors (e.g. his book Decisions and Elections fails to cite Tideman or mention the whole cloning concept!??) and thus regarded Borda as a "success."
Saari's revised condition 3a is, of course, actually the introduction of an estimate of preference strength. The problem is that it regards "number of candidates" as preference strength. If we genuinely introduce preference strength, you get range voting. Indeed, in a paper by Dhillon and Mertens which Saari as usual failed to mention or cite, a revised version of Arrow's conditions, this time reasonable, is used to show that (normalized) range voting is the unique voting system obeying the conditions. Also, range voting obeys Arrow's original "impossible" conditions with some authors' wordings (but not Saari's wording) of the theorem. And Range voting is cloneproof. Saari fails to mention any of that.
The tongue-in-cheek heading here is based on a paper Saari authored "Is approval voting an unmitigated evil?".
The answer (to both questions!) is "no." Saari has good points. When he proves a theorem, it is usually a valid theorem.
But counterexamples exist. E.g. see puzzle 46(a) for an apparently false theorem "proved" by Saari; Saari would not have made this error had he done some computer simulations, but he seems allergic to them. Saari's section 7.2.1 of part II of his January 2000 Economic Theory paper is entirely wrong. It describes (in a way hard to follow unless you understood the whole rest of his development) how to construct N-candidate IRV (instant runoff) elections which are "basic profiles" (i.e. all weighted positional and all pairwise methods agree on the winner and on the finish order) where the IRV winner is the candidate they all rank last, and the IRV elimination order is exactly their finish order, i.e. IRV is maximally insane in the view of all these other voting methods. Saari's construction is inductive on N. The only problem is that his whole claim is false for every N: Proof: IRV cannot eliminate the plurality-voting winner in the first IRV round (and plurality is a weighted positional voting method). Q.E.D. It would be interesting to know what (if anything) can be salvaged from Saari's line of reasoning.Saari sometimes proves some quite difficult and powerful theorems too. He has ability. His voting books are usually pretty fun to read and have educational value. We are just warning the reader to keep in mind the defects of Saari's work, which unfortunately also are numerous. Specifically, his books are neither complete nor unbiased. They indeed – and to a degree which can be absolutely absurd – fail to cite notions and papers showing results which do not conveniently fit into his biased worldview.
Reviewing the above, there is a unified theme. Saari spent his entire voting-research career solving the wrong problems. Sometimes he did so quite impressively (but so what?). And then, once he'd gotten the idea in his head that Borda was the best voting system, he often ignored and refused to cite (large) evidence to the contrary. If other experts wrote to him who had different views, Saari would insult them and refuse to have anything to do with them. (I know, because I personally experienced this, and I keep encountering others who have experienced the same treatment.) That's sad.
What do we mean by "wrong problems"? The right problem is: what is the best voting method? The way to measure "best" is: Bayesian Regret. This is a large framework within which somebody like Saari could have worked.
As far as I can tell (2008), in Saari's entire (large) publication record, he has never mentioned Bayesian Regret. Ever. Not to praise it, not to criticize it, not to use it at all. I see no evidence he even knows what it is. Indeed, Saari stated during his April 2008 radio appearance he had never read my paper on the subject, despite me bringing it to his attention years previously and him telling me what an idiot I was for writing that paper.
Therefore, without the right yardstick for measuring voting system quality, Saari was forced to employ other, wrong, yardsticks. (Not once in his entire opus did Saari ever make a serious comparative consideration of what a "good yardstick" even would be. As far as I can see, he simply assumed whatever felt intuitively interesting to him, must be a good one.) Examples of wrong yardsticks include: requiring "reversal symmetry." Or requiring a small "dictionary." Or demanding rank-order voting or demanding weighted-positional voting systems while ignoring all others for no reason. These all were moves Saari made at one point or another. Now reversal symmetry sounds good, and presumably has some correlation with something good. But it is not the right thing. And a small dictionary also presumably has some correlation with something good. But it too is not the right thing. (To make an analogy, it is something like deciding grocery store A is better than B because it stocks more kinds of food, while ignoring the quality, price, and demand for those foods. Some correlation with the right judgment? Yes. The right judgment? No. And if you define 90% of all grocery stores not to "be" grocery stores because they do not have a red sign, that makes things worse...) And no matter how many times Saari creates some odd definition of some measure of voting system goodness, and then tries to optimize it, and no matter how ingenious he is when he does so, it will still be solving the wrong problem unless he (one day) makes connection to the correct yardstick, Bayesian Regret. Which Saari, so far, apparently does not understand. One could conjecture that this is because Saari is uneducated about Bayesian statistics and utility theory, which is the area that formulates notions of what it is to be "best."
Not only did Saari employ the wrong yardstick, he also in most or all of his work, optimized that wrong yardstick within a teeny tiny subclass of all voting systems, the weighted positional systems. He then often, in public statements, pretended that subclass was actually the full class. That is simply false. Here is a recent example. In a 15 October 2008 interview of Saari in IndyWeek, Fiona Morgan asked
Q. What system would best reflect voters' views?
Saari's answer: This is a mathematical problem that took well over 200 years to be resolved. I solved it within the last several years. It turns out that the system that most accurately reflects the views of the voters is the Borda count.
That was Saari's full statement. It not only is undefined (what might "most accurately reflects" mean?) it also has the disadvantage of being false. To see that, consider for maximum simplicity, an election with only single voter. The voter with Borda rank-orders all the candidates, e.g. Bush=2, Nader=1, Gore=0. With Range Voting she provides scores for all candidates, e.g. Bush=9, Nader=8, Gore=0. Which is a "more accurate reflection" of the views of that one voter?
And again in a video-recorded lecture "Chaotic Elections" by Saari as the "Scope lecture" on 11 October 2008 at NC State University, he says at 46:46, "The Borda count is the unique choice where the outcomes reflect the voters' views." At 49:31 he was asked "Do I understand you right that a true fair election is to do it by the Borda count?" His answer: "Correct. The Borda count has some anomalies, but we know what they are and we know how to handle them. Any other procedure you have – any other procedure – there is a strong probability that you are going to have an outcome which does not satisfy any consistency statement... where the outcome just clearly is off." This answer by Saari is false and unjustified because his repeated-for-emphasis phrase "any other procedure" is false since his work only was able to consider an extremely tiny subset of all procedures, in particular excluding range voting.
What does Saari think of range voting? In the same lecture at 56:40, Saari was asked about strength of preference. The questioner indicated "Mother Teresa" might be a lot better than somebody, not just 'better,' and Borda offers no way for a voter to indicate that" (unlike range voting). Saari then responds that the system where you have 10 points and can allocate them any way you want (this vague description sounds like cumulative voting) is unbelievably bad. Why do we know it is bad? "Because a version of it was used in figure skating." (Strange: Saari now seems to be mentally switching from cumulative to range voting without realizing they differ? Or without realizing that this difference might be important?) Then Saari laughs and says "enough said." That was his full answer. However, I'm afraid I cannot agree with Saari that this answer suffices. Indeed, figure skating after switching away from range voting got repeatedly embarrassed by events in which A finished ahead of B... until C skated, at which point magically the system decided B was ahead of A. That problem cannot happen with either ordinary or trimmed-mean range voting but can and does happen with Borda. The figure skating association finally decided this "switcheroo" behavior was unacceptable, i.e. Borda was unacceptable, and they switched to another system designed to eliminate it. (However, the replacement was misdesigned and thus actually did not eliminate it, but that is another story.)
I've put this bluntly. At the bottom it is simple. Saari keeps solving the wrong problem in a teeny tiny (so tiny it is almost irrelevant) subclass of all voting systems. He is quite able at it. He then announces his solutions very loudly to all kinds of Media, publishes Books, and gets a lot of attention, all the while pretending he has solved The Great Problem open for 200 years of finding The Best Voting System, and wonder of wonders, it is the (embarrassingly bad) Borda system. He then repeats the process. Saari is by no means the only voting researcher who has solved problems and proved various voting systems "optimal" in various (also wrong) senses. Indeed, I think the Condorcet/Young optimality theorem for Condorcet voting is considerably more appealing than Saari's Borda theorems – the sense in which it is "optimal," which concerns "probability of electing the 'wrong' winner" rather than Bayesian Regret, is still wrong but seems closer to what matters than e.g, Saari's "dictionary size." Saari generally does it for Borda voting and the others for other voting systems (and then Saari generally refuses to cite those other works). Saari just tries to get, and gets, more attention than most.
Donald G. Saari:
A dictionary of voting paradoxes, Journal of Economic Theory 48,2 (1989) 443-475.
Explaining all Three-Alternative Voting Outcomes,
J.Econ.Th. 87 (1999) 313-355.
Mathematical structure of voting paradoxes,
I. Pairwise votes, Economic Theory 15,1 (2000) 1-53.
II. Positional voting, Economic Theory 15,1 (2000) 55-102.
Decisions and Elections: Explaining the Unexpected,
Cambridge University Press, 2001.
Geometry of Voting, Springer Verlag, 1994.
Saari has published somewhere in the neighborhood of 50 papers on voting. But the papers listed above constitute (what apparently Saari regards as) his greatest accomplishment: they reach an essentially complete understanding of the full set of every logical "Saari-paradox-type" suffered by every weighted positional rank-order voting method (and his techniques also tell us quite a lot about paradox types in certain other kinds of rank-order-ballot voting methods too). Saari shows that every Saari-paradox-type suffered by the "Borda count" is also suffered by every weighted positional voting method, so that Borda is the one with the fewest paradox-types. Indeed, Saari shows that almost every weighted positional method suffers every thinkable kind of paradox. In the 3-candidate case, every weighted positional method except Borda suffers every thinkable kind of paradox (according to Saari's notion of what a "paradox-type" is – which is however an incomplete notion since for example non-monotonicity is a kind of paradox inadmissible as far as Saari's enumeration is concerned).